Mundo dos Números

Teoria de grupos

Um grupo é um conjunto $G$ munido de uma operação $\circ: G \times G \to G$ tal que:

i)Para todo $g,h, k \in G$ temos $g\circ(h \circ k) = (g \circ h)\circ k$ (Associatividade)
ii)Existe um elemento $e \in G$ tal que $g \circ e = e \circ g = g$ para todo $g \in G$.
iii)Para cada $g \in G$ existe um elemento $g^{-1} \in G$ tal que $g \circ g^{-1} = g^{-1} \circ g = e$

Se, além disso, $g \circ h = h \circ g$ para todo $h \in G$ então o grupo é dito abeliano.

Espaços topológicos

A reta

O conjunto dos números reais $\mathbb{R}$ com a operação de soma é um grupo (abeliano). Este é um exemplo de grupo de ordem infinita, ou seja, tem infinitos elementos. Escrevemos, assim $|G| = \infty$. Outro conjunto numérico que é um grupo é o conjunto dos números complexos sem o zero $\mathbb{C}^{*}$ com a operação de produto. Escrevemos $(\mathbb{C}^{*}, .)$ para denotar o grupo munido da operação.

As raízes da Unidade

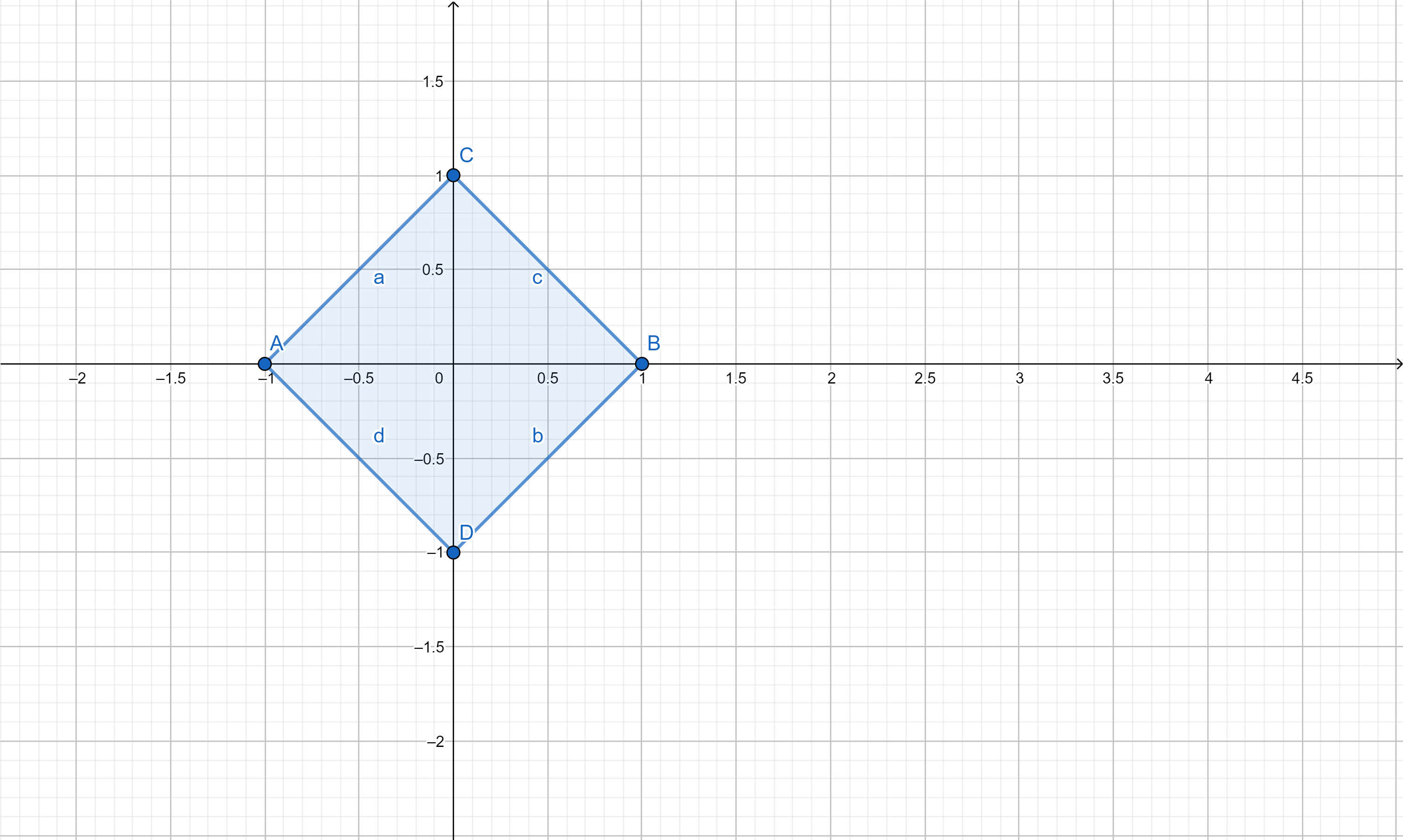
Vamos dar agora um exemplo de um grupo finito. Fixe um $n \in \mathbb{N}$. Uma raiz n-ésima da unidade é um número $z \in \mathbb{C}$ tal que $z^n = 0$. Temos que o conjunto de todas as raízes da unidade é um grupo (com a operação de produto de números complexos). E o mais legal vêm agora: esses números tem uma forma especial. Eles são da forma $$z_k = e^{\frac{2k\pi i}{n}}$$ com $k = 0, \ldots, n-1$. Ou seja, o conjunto das raízes n- ésimas da unidade é: $$\{e^{\frac{2k\pi i}{n}}| k = 0, \ldots, n-1\}$$. Quer mais ? Os elementos desse grupo formar um polígono no plano complexo. Por exemplo, para $n = 4$ temos a seguinte representação:

raiz

Espaços topológicos

Espaços topológicos são conjuntos munidos de uma estrutura que chamamos de Topologia. Basicamente é a estrutura que define o conceito de continuidade e aonde você pode calcular, por exemplo, calcular expressões do tipo \[\lim_{x \to \infty} e^{\cos(x^2)+1}\]. Para formalizar essa ideia é preciso um pouco de trabalho. Por isso daremos algumas definições relâmpago

Uma topologia para um conjunto $X$ é uma coleção $\tau$ de subconjuntos de $X$, chamados de abertos, tais que:

i)$\emptyset$ e $X$ $\in \tau$
ii)Se uma coleção qualquer de conjuntos $\{U_{\lambda}\}_{\lambda \in L} \in \tau$ para todo $\lambda \in L$ então $\bigcup_{\lambda \in \lambda} U_{\lambda} \in \tau$
iii)Se uma coleção finita de conjuntos $\ \{U_n\}_{n \in M} \in \tau$ para todo $n \in M$ então $\bigcap_{n \in M} U_{n} \in \tau$

Os conjuntos de $\tau$ são chamados de Abertos. Um espaço topológico é um conjunto munido de uma topologia

Exemplos legais de Espaços topológicos

Novamente, a reta

A topologia neste caso é a coleção de todos os intervalos abertos. Um intervalo aberto é um conjunto da forma $(a,b)= \{x \in \mathbb{R}| a \le x \le b\}$. Por exemplo, o intervalo $(0,1)$ (o intervalo mais importante de matemática, diga-se de passagem) é o conjunto de todos os números reais maiores que zero e menores que 1.